En nuestra cultura tendemos a etiquetarlo todo; puede que sea la alargada herencia de Aristóteles, el gran clasificador de casi todo, la que nos impulsa a definir cada cosa como " lo que es", y cuya "esencia" nos permite distinguirla de otras diferentes. Es decir, lo "categorizamos" todo, incluidas las ciencias o los saberes varios. Y por ello nos cuesta mucho pensar que las matemáticas y la filosofía puedan compartir un espacio común. O la filosofía y la química. O la Medicina y la filosofía, porque....¿La filosofía una ciencia? Ja, ja. O todo lo contrario.
Ya hablamos de Thales de Mileto, primer filósofo, pero también un reconocido matemático y astrónomo. Descartes te ha acompañado toda la vida con los dichosos "ejes cartesianos" donde has representado infinidad de cosas, y al mismo tiempo, es el fundador del Racionalismo y a filosofía moderna. El filósofo Leibniz disputa con el mismo Newton la "paternidad" del cálculo infinitesimal, al que llegaron, por vías distintas - uno en Alemania y el otro en Gran Bretaña - a unos planteamientos muy similares. Bertrand Russell es conocido por sus "Principia Mathematica", escritos junto a Whitehead, pero es también un reputado filósofo que escribe acerca de la felicidad, el conocimiento humano o lógica. ¿Y qué decir de Wittgenstein, ingeniero aeronáutico que revolucionó la filosofía no una, sino dos veces? La primera con su Tractatus Logico- Philosophicus, unas breves 70 páginas que repasan el lenguaje, el conocimiento, las matemáticas, la metafísica y abren la puerta a la ética. Con todo este párrafo quiero decirte que tratar de establecer compartimentos estancos entre las diferentes ciencias es tan inútil como tratar de descubrir las fronteras de los países en una fotografía aérea.
En la Antigua Grecia hay toda una Escuela de Filosofía que conoces de sobra gracias a las matemáticas. Es la de Pitágoras, la Escuela Pitagórica - aunque algunos la definen como secta, ya que tiene profundas connotaciones políticas, éticas y religiosas, sigo la exposición de Ana Lorca García, alumna del IES Benejúzar que expuso, junto a Álvaro Heredia Lidón los aspectos esenciales de estos pensadores - el "experimento"más fructífero de matemáticas y filosofía.
PITÁGORAS Y LOS PITAGÓRICOS.-
Pitágoras nació en Samos en el año 530 a C. Creó una escuela o comuna, una especie de orden religiosa organizada mediante reglas , y cuya finalidad era llevar a cabo un determinado tipo de vida: contemplativa, generosa, compartiendo todos los descubrimientos. Es decir hay una propuesta ética, que está ligada a su concepción del alma, que entendían como inmortal y que, por tanto, está sometida a la transmigración de un cuerpo a otro (lo que se denomina "metempsícosis". Según esta teoría - cuyos orígenes pudo encontrar Pitágoras en Egipto, donde viajó, o en el orfismo practicado en Grecia - el alma tendrá un destino "mejor o peor" en las siguientes reencarnaciones según sea la vida anterior que ha llevado; por ello, Pitágoras defiende que una vida dedicada al conocimiento es la única que puede llevar a nuestra alma a purificarse y así , aspirar a un destino mejor en subsiguientes tránsitos.Platón tomará esta teoría pitagórica, y será un punto importante en su filosofía.
Pero, ¿Qué dicen los pitagóricos acerca del problema inaugural de la filosofía, esto es, la explicación del cambio y la permanencia en el mundo físico? Pues su respuesta es muy sorprendente de entrada...ya que afirman que la razón inmutable debajo de todo cambio (vamos, el arché) es el NÚMERO. Pues así, pensamos que hay truco, puesto que el número como arché, ¿qué significa?.
En primer lugar, aclaremos que cuando nosotros hablamos de número, tenemos en la mente los números arábigos, o más exactamente indoarábigos - tal como recoge la Wikipedia - , ya que fueron inventados en la India, pero llegaron a Europa a través de los árabes, y se trata de un sistema de numeración posiciones y que ya contaba con el número 0. De la India pasaron a Persia, y de ahí los tomaron los árabes, usándolos en el norte de África, de donde pasaron a Europa durante las invasiones de la Edad Media. Los griegos usaban las letras del alfabeto, al igual que los romanos hicieron también, pero se ayudaban de piedras y líneas para hacer sus operaciones, y así puedes ver los números que están representados más arriba: imagina que son piedrecitas agrupadas. Por cierto, la palabra piedra en latín era "calculus", de la que deriva Cálculo, esa rama de las Matemáticas que lidia con los números y las operaciones que con ellos realizamos.Todo esto se viene a resumir en que cuando un griego habla de números, tiene en su mente unos puntos armónicamente dispuestos en el espacio (claro, si están dispuestos al tun tún, nos encontramos con un puñado de guijarros, pero no con el número).
Los pitagóricos fueron los primeros en teorizar acerca de los números, aunque para ellos, los números eran entendidos más de una forma cualitativa que cuantitativa, y por ello pensaban que el número 1 representaba la permanencia; el 2, la opinión mudable, el 4 la justicia y el 10 la perfección .
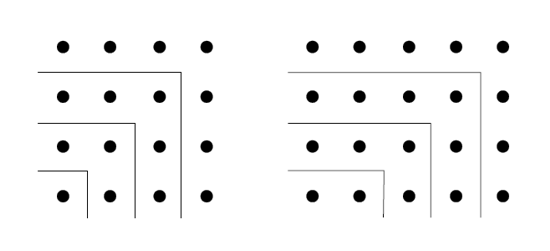
También atribuyen distinto grado de perfección a los números según sean pares o impares, dado que tal y como los representaban, los números impares, eran cuadrados - y por ello más perfectos -, mientras que los pares, que se representaban mediante rectángulos lo eran menos. Inserto una imagen de cómo se representaban los números pares e impares:
El número perfecto es el 10 (tetraktys), ya que es un triángulo equilátero que contiene igual número de pares que impares sin que predomine ningún elemento, y contiene igual cantidad de números primos que divisibles.
Fíjate ya el grado de abstracción que ha conseguido la Filosofía en poco tiempo: de pensar que todo obedece al capricho de los dioses inmortales, se hace un esfuerzo por reducir los ciclos de la naturaleza a nociones abstractas y a figuras geométricas; el logos ha hecho un largo camino.
Se cuenta que las reflexiones acerca del número le vienen a Pitágoras por sus reflexiones sobre la música, desencadenadas por el sonido de los martillos en una fragua. Cuentan que Pitágoras paseaba un día por la calle, y al pasar cerca de una fragua, notó que el sonido de los martillos al golpear el hierro candente eran diferentes según fuese el tamaño del martillo y el lugar donde se propinase el golpe. De ahí pasó a establecer la primera teoría de armonía musical tras experimentar con instrumentos de cuerdas, y ello no significa nada más - y nada menos - que la música es sonido "disciplinado" por el número, la proporción.
La música es armonía. Y ahora fíjate en esto: el lenguaje musical se escribe en un pentagrama, donde colocamos "bolas" (notas) blancas y negras dispuestas en un orden preciso para que, al traducirlas al material del instrumento, este suene de una forma armónica y no simplemente haciendo ruido. Pondremos una pentagrama para ver:

Ya hablamos de Thales de Mileto, primer filósofo, pero también un reconocido matemático y astrónomo. Descartes te ha acompañado toda la vida con los dichosos "ejes cartesianos" donde has representado infinidad de cosas, y al mismo tiempo, es el fundador del Racionalismo y a filosofía moderna. El filósofo Leibniz disputa con el mismo Newton la "paternidad" del cálculo infinitesimal, al que llegaron, por vías distintas - uno en Alemania y el otro en Gran Bretaña - a unos planteamientos muy similares. Bertrand Russell es conocido por sus "Principia Mathematica", escritos junto a Whitehead, pero es también un reputado filósofo que escribe acerca de la felicidad, el conocimiento humano o lógica. ¿Y qué decir de Wittgenstein, ingeniero aeronáutico que revolucionó la filosofía no una, sino dos veces? La primera con su Tractatus Logico- Philosophicus, unas breves 70 páginas que repasan el lenguaje, el conocimiento, las matemáticas, la metafísica y abren la puerta a la ética. Con todo este párrafo quiero decirte que tratar de establecer compartimentos estancos entre las diferentes ciencias es tan inútil como tratar de descubrir las fronteras de los países en una fotografía aérea.
En la Antigua Grecia hay toda una Escuela de Filosofía que conoces de sobra gracias a las matemáticas. Es la de Pitágoras, la Escuela Pitagórica - aunque algunos la definen como secta, ya que tiene profundas connotaciones políticas, éticas y religiosas, sigo la exposición de Ana Lorca García, alumna del IES Benejúzar que expuso, junto a Álvaro Heredia Lidón los aspectos esenciales de estos pensadores - el "experimento"más fructífero de matemáticas y filosofía.
PITÁGORAS Y LOS PITAGÓRICOS.-
Pitágoras nació en Samos en el año 530 a C. Creó una escuela o comuna, una especie de orden religiosa organizada mediante reglas , y cuya finalidad era llevar a cabo un determinado tipo de vida: contemplativa, generosa, compartiendo todos los descubrimientos. Es decir hay una propuesta ética, que está ligada a su concepción del alma, que entendían como inmortal y que, por tanto, está sometida a la transmigración de un cuerpo a otro (lo que se denomina "metempsícosis". Según esta teoría - cuyos orígenes pudo encontrar Pitágoras en Egipto, donde viajó, o en el orfismo practicado en Grecia - el alma tendrá un destino "mejor o peor" en las siguientes reencarnaciones según sea la vida anterior que ha llevado; por ello, Pitágoras defiende que una vida dedicada al conocimiento es la única que puede llevar a nuestra alma a purificarse y así , aspirar a un destino mejor en subsiguientes tránsitos.Platón tomará esta teoría pitagórica, y será un punto importante en su filosofía.
Pero, ¿Qué dicen los pitagóricos acerca del problema inaugural de la filosofía, esto es, la explicación del cambio y la permanencia en el mundo físico? Pues su respuesta es muy sorprendente de entrada...ya que afirman que la razón inmutable debajo de todo cambio (vamos, el arché) es el NÚMERO. Pues así, pensamos que hay truco, puesto que el número como arché, ¿qué significa?.
En primer lugar, aclaremos que cuando nosotros hablamos de número, tenemos en la mente los números arábigos, o más exactamente indoarábigos - tal como recoge la Wikipedia - , ya que fueron inventados en la India, pero llegaron a Europa a través de los árabes, y se trata de un sistema de numeración posiciones y que ya contaba con el número 0. De la India pasaron a Persia, y de ahí los tomaron los árabes, usándolos en el norte de África, de donde pasaron a Europa durante las invasiones de la Edad Media. Los griegos usaban las letras del alfabeto, al igual que los romanos hicieron también, pero se ayudaban de piedras y líneas para hacer sus operaciones, y así puedes ver los números que están representados más arriba: imagina que son piedrecitas agrupadas. Por cierto, la palabra piedra en latín era "calculus", de la que deriva Cálculo, esa rama de las Matemáticas que lidia con los números y las operaciones que con ellos realizamos.Todo esto se viene a resumir en que cuando un griego habla de números, tiene en su mente unos puntos armónicamente dispuestos en el espacio (claro, si están dispuestos al tun tún, nos encontramos con un puñado de guijarros, pero no con el número).
Los pitagóricos fueron los primeros en teorizar acerca de los números, aunque para ellos, los números eran entendidos más de una forma cualitativa que cuantitativa, y por ello pensaban que el número 1 representaba la permanencia; el 2, la opinión mudable, el 4 la justicia y el 10 la perfección .
También atribuyen distinto grado de perfección a los números según sean pares o impares, dado que tal y como los representaban, los números impares, eran cuadrados - y por ello más perfectos -, mientras que los pares, que se representaban mediante rectángulos lo eran menos. Inserto una imagen de cómo se representaban los números pares e impares:
El número perfecto es el 10 (tetraktys), ya que es un triángulo equilátero que contiene igual número de pares que impares sin que predomine ningún elemento, y contiene igual cantidad de números primos que divisibles.
Fíjate ya el grado de abstracción que ha conseguido la Filosofía en poco tiempo: de pensar que todo obedece al capricho de los dioses inmortales, se hace un esfuerzo por reducir los ciclos de la naturaleza a nociones abstractas y a figuras geométricas; el logos ha hecho un largo camino.
Se cuenta que las reflexiones acerca del número le vienen a Pitágoras por sus reflexiones sobre la música, desencadenadas por el sonido de los martillos en una fragua. Cuentan que Pitágoras paseaba un día por la calle, y al pasar cerca de una fragua, notó que el sonido de los martillos al golpear el hierro candente eran diferentes según fuese el tamaño del martillo y el lugar donde se propinase el golpe. De ahí pasó a establecer la primera teoría de armonía musical tras experimentar con instrumentos de cuerdas, y ello no significa nada más - y nada menos - que la música es sonido "disciplinado" por el número, la proporción.
La música es armonía. Y ahora fíjate en esto: el lenguaje musical se escribe en un pentagrama, donde colocamos "bolas" (notas) blancas y negras dispuestas en un orden preciso para que, al traducirlas al material del instrumento, este suene de una forma armónica y no simplemente haciendo ruido. Pondremos una pentagrama para ver:
Si te fijas, verás que tienen bastante parecido esta imagen y la anterior. Parece que todo empieza a encajar.
Nos queda un elemento más para entender la visión pitagórica, y este no es otro que el Universo entendido como Cosmos, es decir, lugar ordenado, armónico. Hablar del Universo en el mundo griego es hablar de un espacio bastante más reducido que el nuestro, ya que las observaciones eran únicamente hechas con los ojos, sin ningún instrumento, y por ello, lo que veían eran puntos colocados en unas posiciones regulares en la bóveda celeste. ¡Ahí tenemos de nuevo los puntos!. Y además de ellos, tenemos que gracias a los avances teóricos de Tales y de los Pitagóricos, se pueden calcular distancias y volúmenes de los cuerpos celestes, resultando..¡Que responden a la misma proporción que la que producía la armonía de la música, y que se traducía en la teoría de los cuadrados! Por ello, Pitágoras afirmaba que el número ( la armonía) era el denominador común racional de toda la naturaleza, el arche´.
Para acabar, su teoría cosmológica acaba de una forma bellísima: para Pitágoras los volúmenes distancias entre los cuerpos celestes guardan la proporción aúrea, la base de la armonía; cada cuerpo celeste es una nota, y al girar todo el conjunto al mismo tiempo, hace sonar una melodía conocida como " música de las esferas", audible, pero imperceptible para nosotros, puesto que la estamos oyendo desde nuestro nacimiento. En este punto, hay una relación con la ciencia actual y la rediación de microondas que se oye de fondo en todo el universo, aunque nosotros no podamos percibirla por estar siempre ahí.
No hay comentarios:
Publicar un comentario